Presentation – Page 2 – Mike Pawliuk

Another Combinatorial Result

Here is Chris Eagle’s presentation from Stevo Todorcevic’s class “Combinatorial Set Theory”.

From the abstract:

We prove that MA + $\mathfrak{c} = \aleph_2$ implies $\mathfrak{c} \not\rightarrow (\mathfrak{c}, \omega+2)^2$ . The exposition is based on hand-written notes provided by S. Todorcevic. The result itself is due to R. Laver.

This is the analogous result to “MA implies (NonSpecial Tree) $\not\rightarrow$ (NonSpecial Tree, $\omega+2)^2$ “, which I explained here.

Facts about the Urysohn Space – Some useful, some cool

(This is almost verbatim the talk I gave recently (Feb 23, 2012) at the Toronto Student Set Theory and Topology Seminar. I will be giving this talk again on April 5, 2012)

I have been working on a problem involving the Urysohn space recently, and I figured that I should fill people in with the basic facts and techniques involved in this space. I will give some useful facts, a key technique and 3 cool facts. First, the definition!

Definition: A metric space $U$ has the Urysohn property if

$U$ is complete and separable

$U$ contains every separable metric space as an isometric copy.

$U$ is ultrahomogeneous in the sense that if $A,B$ are finite, isometric subspaces of $U$ then there is an automorphism of $U$ that takes $A$ to $B$ .

You might already know a space that satisfies the first two properties – The Hilbert cube $[0,1]^\omega$ or $C[0,1]$ the continuous functions from $[0,1]$ to $[0,1]$ . However, these spaces are not ultrahomogeneous. Should a Urysohn space even exist? It does, but the construction isn’t particularly illuminating so I will skip it.

Continue reading Facts about the Urysohn Space – Some useful, some cool

MA and its effect on Tree Partitions

(This is the presentation I gave for Stevo Todorcevic’s course Combinatorial Set Theory on Feb 28, 2012. The material comes from Stevo’s 1983 paper “Partition Relations for Partially Ordered Sets”.)

In partition relations for ordinals, it has been established that:

Theorem (Erdos-Rado). 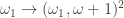$\omega_1 \rightarrow (\omega_1, \omega+1)^2$

Later it was shown that this is the best you can do, as the strengthenings are consistent:

Theorem(Hajnal). Under CH, 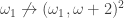$\omega_1 \not\rightarrow (\omega_1, \omega+2)^2$
Theorem (Todorcevic). Under PFA, for any countable ordinal $\alpha$ , $\omega_1 \rightarrow (\omega_1, \alpha)^2$

Moving on, we can ask the same questions about non-special trees, which in some way are the tree analogue of “uncountable” or “large”.

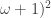
Theorem (Todorcevic). Nonspecial Tree $\rightarrow$ (Nonspecial Tree, $\omega+1)^2$

This is the analogue or the Erdos-Rado theorem.

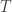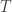Recall that a tree $T$ is nonspecial if $T \rightarrow (\omega)^1_\omega$ , which means that any countable partition $T$ contains an infinite set. (This is a generalization of uncountable, because for countable sets you can always put one element per colour.)

We will show the following:

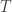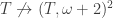Theorem (Todorcevic). Under MA, for $T$ a tree with no uncountable chains and $\vert T \vert = 2^{\aleph_0}$ we have $T \not\rightarrow (T, \omega+2)^2$ .

Continue reading MA and its effect on Tree Partitions