Mike Pawliuk – Mathematics – Page 6 – Assistant Professor, Teaching Stream, at the University of Toronto Mississauga

Ropes and Dwarfs in a Munich Subway

People in Germany like Math! After my recent trip to Bonn, Germany, I visited my friend Maria in Munich, Germany for a weekend. She was wonderful and showed me all around town. One thing about her that has always impressed me was how into mathematics she is. When I met her in Toronto last year, I distinctly remember thinking that her interest in mathematics (she is a PhD student in Classics) came from her German education. My trip to Munich only reinforced this.

Continue reading Ropes and Dwarfs in a Munich Subway

Secret Santa 4: The Surprise

After a long hiatus (7 months!) I am finally back to writing. This week I revisited an old problem that Sam Coskey told me a couple of years ago. Some of you will remember this “Secret Santa problem”, which I wrote about before. The problem is:

Sam’s Problem. Is it possible for two people to each choose a natural number so that both numbers are exactly 1 apart and neither person knows who has the larger of the two numbers?

Continue reading Secret Santa 4: The Surprise

Using Dushnik-Miller to prove that every sigma-compact group is ccc

(This is the write-up for a talk I gave in the Toronto Student Set Theory and Topology seminar on May 2, 2013.)

A couple of weeks ago I gave a talk for the set-theoretic topology course I was in, on the topic of cardinal invariants of topological groups. While I was preparing that presentation I discovered the following fact:

Theorem [Tkachenko, 1983] Every 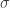$\sigma$ -compact group is ccc.

I will present a proof that I have adapted from Tkachenko’s original paper (“Souslin property in free topological groups on bicompacta”) and the proof that appears in Arhangel’skii & Tkachenko’s big purple book (Section 5.3 of Topological Groups and Related Structures). Both proofs involve first proving a Ramsey result about covers of a space, then using this to prove that a particular space has “weak-precalibre $\aleph_1$ ” (i.e. Property K) which is a property that implies ccc. Learning this proof has been part of my ongoing attempt to learn how Ramsey results show up in topology.

Continue reading Using Dushnik-Miller to prove that every sigma-compact group is ccc

A Survey of Cardinal Invariants of Topological Groups

(This is a presentation I gave for Bill Weiss’ course Set-Theoretic Topology on April 19, 2013. In class we discussed some cardinal invariants and how they are related; here I will survey what happens when we look at the cardinal invariants of topological groups.)

This review follows very closely the discussion in section 5.2 of Arhangel’skii and Tkachenko’s book “Topological Groups and Related Structures“. Another good resource is section 3 of Comfort’s article “Topological Groups” in the Handbook of Set-Theoretic Topology. The only thing I claim to be my own are the (unsourced) pictures I have provided.

Continue reading A Survey of Cardinal Invariants of Topological Groups

Kangaroo Contest 2013 Talk about Cryptography

On Sunday March 24, 2013, I gave a talk on the History of Cryptography [PDF], at the University of Toronto (Scarborough) for the parents of students writing the Kangaroo Contest. I had many questions after my talk, so here are some answers to the questions I received.

Where did you get this information?

Most of this talk came from Elementary Number Theory by David M. Burton, the Wikipedia article for RSA, and the Wikipedia article for Diffie-Hellman. As a general rule of thumb, Wikipedia is a reliable source for things of a mathematical nature (as only experts tend to edit the articles).

My child is interested in codes, what are some resources for them to learn more?

Here is a great introduction to modular arithmetic which serves as the foundation for learning about the math of cryptography. Modular arithmetic is like “clock math”, where 4 hours after 10 o’clock is 2 o’clock.

Codecademy is a very good way to start learning computer programming. It is a very fun website and is very motivating, and fun!

Continue reading Kangaroo Contest 2013 Talk about Cryptography

My Presentation on T-sequences for the Toronto Set Theory Seminar

On February 15, 2013, I gave a talk entitled “A robust family of topological groups on $\mathbb{Z}$ “.

Here are my slides.

Let’s Make Some T-sequences

(This was the basis for a talk I gave at the Toronto Student Set Theory and Topology seminar on January 15, 2013. The assumed knowledge is an undergraduate course in general topology. This is only a draft, and will be updated soon.)

Introduction

There are many questions in mathematics and sciences in general whose main object of study is the topological group. These objects are very versatile and can represent many of the structures we encounter. One question that I’ve been working on examines the (extreme) dynamical properties of topologies on the integers. On the recommendation of Vladimir Pestov (one of my advisors) I have been learning about T-sequences, which provide a rich method for producing topological groups with extreme behaviour. Here I will present two techniques involving T-sequences that help to answer two different questions about topological groups; one is about dynamics and the other is about combinatorial properties of $\mathbb{N}^\N$ . These results all come from “Topologies on the Integers” by Protasov and Zelenyuk.

Continue reading Let’s Make Some T-sequences

Math Anxiety

A study was done at the University of Chicago looking at whether math can cause physical pain. (The rather laughable title of the article is “Doing Math Really Does Make Your Head Hurt, Says Science”. Here‘s the actual published study.)

The idea is that for people with high levels of math anxiety, just knowing that they are about to do a math problem is enough to make the pain part of their brain go off. The actual solving of the problem wasn’t such a big deal. This suggests that presenting math is an important part of teaching it and discussing it.

Some other anecdotal examples are that people are notoriously good at calculating retail discounts – “It will be 12.50 for that 25 dollar shirt that is half off”. Compare this to the more difficult “What is 25 divided by 2?” or even worse “What is 25 x 0.5?”.

Similarly compare these two questions:

After the half-hour 6 o’clock news you watch an episode of Jeopardy, then Survivor, then two episodes of Wheel of Fortune. You read until it’s a quarter to 10 and then go to bed. How long did you read before you went to bed?
Here’s an easy question about fractions: Solve 6 + 1/2 + 1/2 + 1 + 2 (1/2) + R = 10 – 1/4.

I got a little bit anxious looking at that second question.

What experiences do you have about teaching people with math-anxiety?

Perceptions about Mathematics

“When someone asks you what you do as a mathematician, they take the most advanced training they have in mathematics and assume that you do a much harder version of that.”

This is a paraphrase of something I will attribute to Leo Goldmakher.

The idea is that if someone has only ever taken high-school math, they might think that mathematicians spend their time multiplying and dividing very large numbers; (“Are you even allowed to use calculators in your work?“). If someone has been lucky enough to take a first-year calculus course they might imagine that mathematicians solve harder and harder related rates questions. Going a step further, telling a mathematician that I study set theory often invokes brow-furrowing and questions like: “Don’t we already know everything about ordinals and cardinal arithmetic?“.

Stevo’s Forcing Class Fall 2012 – Class 17

(This is the seventeenth (and final) lecture in Stevo Todorcevic’s Forcing class, held in the fall of 2012. You can find the sixteenth lecture here. Quotes by Stevo are in dark blue; some are deep, some are funny, some are paraphrased so use your judgement. As always I appreciate any type of feedback, including reporting typos, in the comments below.)

NOTE: This page is pretty raw as I have not edited it yet. Please tread carefully!

[TITLE]

“I want to go a little over this proof.“

Theorem 1 (Carlson-Laver, 1989). Assuming PFA, $\vDash_\textrm{Sacks} \textrm{MA} (\aleph_1)$ .

Recall the notation:

$\mathcal{S} := \{p \subseteq 2^{<\omega}: p \textrm{ is a perfect tree }\}$ ;
$\mathcal{A} := \{(p,n) : p \in \mathcal{S}, n<\omega\}$ , the Amoeba;
$\dot{\PP}$ is an $\mathcal{S}$ -name for a ccc poset, identified with $\{$ all $\mathcal{S}$ -names for elements of $\dot{\PP}\}$ ;

In $V^\mathcal{A}$ we order $\dot{\PP}$ as follows: $\tau \leq_\mathcal{A} \sigma$ iff $\exists (p,n)$ in the generic filter such that $p \vDash \tau \leq_{\dot{\PP}} \sigma$ .
Aside: We can assume $\dot{\PP} = (X^\smile, \leq_\mathbb{P}), X \subseteq 2^\omega, \vert X \vert \leq \aleph_1$ and $\tau : 2^\omega \rightarrow 2^\omega$ is continuous such that $\textrm{int}_G (\tau) = \tau(\textrm{sacks real})$ .

“I would like to show this is a ccc poset.”

Claim 2: [In $V^\mathcal{A}$ ] $(\dot{Q}, \leq_\mathcal{A})$ is a ccc poset.
We actualy need claim 0. (Remember claim 1 was about a caliber property.)

Claim 0: For every sequence $\{\tau_\alpha : \alpha < \omega_1\}$ of elements of $\dot{Q}$ and $p \in \mathcal{S}$ there is an uncountable $\Gamma \subseteq \omega_1$ and a family $\{p_\alpha : \alpha \in \Gamma\}$ of pairwise compactible elements of $\mathcal{S}$ below $p$ such that:
$\displaystyle p_\alpha \wedge p_\beta \not \vDash \tau_\alpha \perp \tau_\beta$

(“Double negation!“)

proof of Claim 0.

Apply PFA to $\mathcal{S} \star \dot{\PP}$ which will force uncountably many generics into ‘the set'(???). [End of proof]

proof of Claim 2.

Let $\{\tau_\alpha : \alpha < \omega_1\}$ of elements of $\dot{Q}$ . By lemma 1, some uncountable subset of $\{\tau_\alpha : \alpha < \omega_1\}$ belongs to $V$ so we may work in $V$ .

So we need to produce $(p,n) \in \mathcal{A}$ (below any given $(q,m) \in \mathcal{A}$ ) and $\alpha \neq \beta$ such that $(p,n)
\vDash_\mathcal{A} \tau_\alpha \not \perp_\mathcal{A} \tau_\beta$.

In fact, $n=m$ . Set:

$\{s_1, ..., s_k\} = q \cap 2^m$ ; and
$q^{s_i} = q \cap \{x \in 2^{< \omega} : x \not \perp s_i\}$ . (“Perfect tree, clopen set.”)

Applying lemma 0, we get an uncountable $\Gamma_1 \subseteq \omega_1$ and $\{p_\alpha^1 : \alpha \in \Gamma_1\} \subseteq \mathcal{S} \upharpoonright q^{s_1}$ such hat
$\displaystyle \forall \alpha, \beta \in \Gamma_1, \textrm{ we have } p_\alpha^1 \wedge p_\beta^1 \not \vDash \tau_\alpha \perp \tau_\beta$

Apply lemma 0 again to find an uncountable set $\Gamma_2 \subseteq \Gamma_1$ and $\{p_\alpha^2 : \alpha \in \Gamma_2\} \subseteq \mathcal{S} \upharpoonright q^{s_2}$ such that
$\displaystyle \forall \alpha, \beta \in \Gamma_1, \textrm{ we have } p_\alpha^2 \wedge p_\beta^2 \not \vDash \tau_\alpha \perp \tau_\beta$

Now if $\alpha \neq \beta \in \Gamma$ , then for each [… SEE DANA]

“Last time I mentioned these names: Souslin, Sacks, Solovay (random).”

“I decided not to talk about this now as I will be giving a lecture in the Czech Republic in February.”

“[Here is] exposition about two results, actually 3 (one which unifies them) which are actually quite complete.“

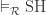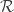Theorem 2 (1985, Laver). $\textrm{MA} (\aleph_1)$ implies $\vDash_\mathcal{R} \textrm{SH}$ , for any measure algebra $\mathcal{R}$ .

“Assuming $\diamondsuit$ isn’t interesting as measure algebras preserve Souslin trees. You’d like to use CH, but the next result says there is no hope.“

Theorem (Hirshurn, 2000). PID implies 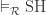$\vDash_\mathcal{R} \textrm{SH}$ .

Ultrapowers of Measure Algebra 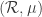$(\mathcal{R}, \mu)$

Let $I$ be an index set, $\mathcal{U}$ a non-principal ultrafilter on $I$ , and consider $(\mathcal{R}^I /\mathcal{U}, \mu_\mathcal{U})$ be the ultrapower where $\mu_\mathcal{U} ([f]_\mathcal{U}) = \lim_{i \rightarrow \mathcal{U}} \mu(f(i))$ .

Theorem (Todorcevic, 1995). If the character (i.e. density of the metric space) of $\mathcal{R}$ is bigger than $I, \theta$ then for every sequence $([f_\xi]: \xi < \theta) \subseteq \mathcal{R}^I /\mathcal{U}$ , there is a sequence $(c_\xi: \xi < \theta) \subseteq \mathcal{R}$ such that:

(“The $c_\xi$ ‘s reflect.“) $\mu (c_\xi) = \lim_{i \rightarrow \mathcal{U}} \mu(f_\xi (i))$ for all $\xi < \theta$ ;
(“More important:”) $\forall K \in \mathcal{U}, \forall \Gamma \in [\theta]^{<\omega}, \bigwedge_{\xi \in \Gamma} c_\xi \leq \bigvee_{i \in K} \bigwedge_{\xi \in \Gamma} f_\xi (i)$

“You should dare to do something. It is a Brave New World.“

Proof of Theorem 2

Proof of Theorem 2. “Once you do the proof, you will see you do not want to check if PID implies $\vDash_\mathcal{R}$ PID.”

Let $(\omega_1, \leq_T)$ be an $\mathcal{R}$ -name for an Aronszajn tree nicely put on $\omega_1$ . I.e. $[\delta, \delta+\omega)$ is its $\delta^\textrm{th}$ level for $\delta$ countable limit.

“This idea comes from the original source for PID.“

$\dot{I}_T = \{X \subseteq \omega_1 : X \textrm{ countable}, X \textrm{ strongly unbounded}\} = \{\textrm{pred}_T (\alpha) : \alpha < \omega_1\}$ , where $X$ is strongly unbounded if every infinite subset of $X$ is unbounded.

$\vDash_\mathcal{R} \dot{I}_T$ is a P-ideal.

“This of course is wht PID implies SH, but not here, because we just have names.“

Let $\mathcal{I} = \{A \subseteq \omega_1 : \llbracket A^\smile \in \dot{I}_T \rrbracket_\mathcal{R} = 1\}$ .

Claim: $\mathcal{I}$ is a P-ideal.

“I strongly suggest you do this with other posets and see if it is P-ideal. e.g. Sacks. Might have something to do with weakly-distributive or $\omega^\omega$ -bounding.”

$\{A_n : n<\omega\} \subseteq \mathcal{I}$ . “What are the pieces to chop off?”

$\bigcup_{n < \omega} A_n \subseteq \delta$ for $\delta$ countable limit.

Let $\dot{A}_{n,k}$ be the $\mathcal{R}$ -name for $\{\alpha \in A_n : \alpha <_T \delta + k\}$ .

For $r,m < \omega$ , choose a _finite_ set $F_{n,m} \subseteq A_n$ such that
$\displaystyle \mu(\llbracket \bigcup_{k \leq n} A_{n,k} \subseteq F_{n,m}^\smile \rrbracket > 1 - \frac{1}{2^m})$

(“i.e. is very close to 1“)

[PICTURE 1]

Let
$\displaystyle A := \bigcup_{m < \omega} (A_m \setminus \bigcup_{n \leq m} F_{n,m})$

Note $A_m \subseteq^* A, \forall m < \omega$ . We need to show this is in $\mathcal{I}$ .

For $m < \omega$ , $A^m := A \cap \bigcup_{n \geq m} A_n$ .

[PICTURE 2]

$\displaystyle \mu(\llbracket \textrm{pred}(\delta + h?) \cap A^m \neq \emptyset \rrbracket < 2^{-m+1})$

(“You don’t need to worry about the $A_n$ ‘s.“)

By PID, we have that either:

There is an uncountable $B \subseteq \omega_1$ such that $[B]^{\aleph_0} \subseteq \mathcal{I}$ . (So $\llbracket B^\smile$ contains an uncountable antichain $\rrbracket = 1$ .)
There is an uncountable $B \subseteq \omega_1$ such that $B \perp \mathcal{I}$ .

( $\star$ ) “Here is where we need this measure theory lemma about ultrapowers.”

“What are the functions?“

Pick a uniform ultrafilter $\mathcal{U}$ on $\omega_1$ such that $B \in \mathcal{U}$ . For $\alpha \in B$ let $f_\alpha : \omega_1 \rightarrow \mathcal{R}$ be defined by $f_\alpha (\beta) = \llbracket \alpha <_T \beta \rrbracket$ .

Claim. $\{\alpha \in B : \lim_{\beta \rightarrow \mathcal{U}} \mu[f_\alpha (B) \neq 0]\}$ is countable.
proof. Otherwise, let $B_0 = \{\alpha \in B : \mu_\mathcal{U}([f_\alpha])>0\}$ .

Apply the ultrapower theorem. We will get some $c_\alpha \in \mathcal{R}$ for ( $\alpha \in B_0$ ) that somehow reflects.
$\displaystyle \forall K \in \mathcal{U}, \forall \Gamma \in [B_0]^{<\omega}, \bigwedge_{\xi \in \Gamma} c_\xi \leq \bigvee_{\beta \in K} \bigwedge_{\alpha \in \Gamma} f_\alpha (\beta)$

(“Here the $<\omega$ is really just 2. Just pairs.“)

“If you decode what I wrote, that’s what it says.”

Find $c \in \mathcal{R}$ such that $c \vDash \{\alpha \in B_0 : c_\alpha \in \textrm{ generic object}\} =: B_1$ is countable.

So $c \vDash \dot{B_1}$ is a branch of $T$ .

“This [ $B_2$ ] is a good name, a fantastic name! I can’t believe I picked such a good name. It is a branch.”

The generic must pick up some $\beta \in K$ for which $\alpha$ [SOMETHING]. So [SOMETHING ELSE]. [End of Proof]

“At ( $\star$ ) I force to add to the density, so the theorem applies. If I broke the Suslin tree, great!“

[SECTION TITLE]

“Let us see that MA( $\aleph_1$ ) is enough to push through SH.”

“People are interested in some Martin principles.”

Statement of SM $_\theta$ . For every *S*et-*M*apping $f: \theta \rightarrow [\theta]^{\leq \aleph_0}$ either:

$\theta = \bigcup_{n < \omega} X_n$ , where each $X_n$ is $f$ -Free.
There is an uncountable $B \subseteq \theta$ such that for every finite $\Gamma \subseteq B$ , $\{\beta \in B : \Gamma \subseteq f(\beta)\}$ is uncountable. (“Very much not free.”)

Compare this with the Free-Set Lemma:

Free-Set Lemma. [STATEMENT]

Theorem (Todorcevic, 1995): MA(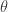 $\theta$ ) implies $\vDash_\mathcal{R}$ SM $_\theta$ , for every measure algebra.

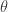Exercise. SM $_\theta$ implies that trees on $\theta$ with no uncountable chains are special.

(Use pred mapping, $f(\beta) = \{\alpha : \alpha <_T \beta\}$ . Use $T=(\theta, <_T)$ , so you kill Suslin trees.)

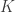Proposition. SM $_{\omega_1}$ implies that if a compact space $K$ contains an L-subspace,then $K$ contains an uncountable free sequence.

Recall. An L-space is a regular, hereditarily Lindelof, non-separable space. (These exist in ZFC.)

Corollary. SM $_{\omega_1}$ implies that perfect compacta are separable.

Proof of Proposition.

Assume $K \subseteq \omega_1$ is an L-space. This means (by possibly passing to a subsequence) that
$\displaystyle \overline{\{\alpha : \alpha < \beta\}}^K \cap \{\alpha : \alpha \geq \beta\} = \emptyset$

By regularity, pick $U_\beta \ni \beta$ open in $K$ such that $\overline{U_\beta}^K \cap \overline{\{\alpha : \alpha < \beta\}}^K$ . Define $f: \omega_1 \rightarrow [\omega_1]^{\leq \aleph_0}$ , by $f(\beta) = \{\alpha : \beta \in U_\alpha\}$ .

“Free set is a discrete space.” (??)

For $B$ in the second alternative we get $\forall \gamma \in B$ , we have that the collection of $\overline{\{\alpha: \alpha < \beta\}}^K$ and $\overline{U_\beta}^K$ (for $\beta \in B \cap \gamma$ ) has the finite intersection property. [End of proof]

Now We Try to Prove the Theorem.

proof. Fix an $\mathcal{R}$ -name $\dot{f}$ for a set-mapping as in SM $_\theta$ . For $\beta \in \theta$ , $\Delta(\beta) := \{\alpha : \llbracket \alpha \in \dot{f}(\beta) \rrbracket > 0\}$ is countable, by measure algebra.

“I want to apply MA $_\theta$ , so I need a poset. The idea seems to be to force [the first alternative], and if it isn’t ccc, then [the second alternative].”

“I will force one free set, but there is the usual trick to get many.“

Let $\mathcal{R}_\beta$ be the subalgebra generated by $\{\llbracket \alpha \in \dot{f}(\beta) \rrbracket : \alpha \in \Delta(\beta)\}$ , which is separable as a metric space.

Poset. Let $\mathbb{P}$ be the collection of all finite partial maps $p: D_p \rightarrow \mathcal{R}$ such that:

$p(\alpha) \in \mathcal{R}_\alpha, \mu(p(\alpha)) > 1/2$ for $\alpha \in D_p$ .
$p(\alpha) \wedge p(\beta) \leq \llbracket \alpha \notin \dot{f}(\beta) \rrbracket$ for $\alpha \neq \beta \in D_p$ .

“[1] is a tricky move. For measure algebras making the requirement rarely gives ccc. But I’m hopeful because I’veput it in the separable algebra $\mathcal{R}_\alpha$ .“

Ordering. $p \leq q$ iff

$D_p \supseteq D_q$ ; and
$p(\alpha) \leq q(\alpha)$ for $\alpha \in D_q$ .

“If it is (powerfully) ccc, you are forcing alternative 1.”

“So we focus on alternative 2.“

Claim. If $\mathbb{P}$ is not ccc, then there is an $\mathcal{R}$ -name $\dot{B}$ for an uncountable subset of $\theta$ satisfying the second alternative of SM $_\theta$ .

“First a $\Delta$ -system, etc.“

Let $(p_\alpha : \alpha < \omega_1) \subseteq \mathbb{P}$ be a sequence of pairwise incompatible elements in $\mathbb{P}$ .

“Now we have to be careful.”

Fix $\xi \in D$ , $p_\alpha (\xi)$ for $\xi < \omega_1$ , sitting in $\mathcal{R}_\xi$ a separable [SOMETHING SOMETHING].

So [SOMETHING], we can ignore the root.

“Now the u.p. thing.“

Suppose $p_\alpha (\xi) > 1/2 \neq \epsilon ?$ , for all $\xi \in D_p$ , $\xi \in \Gamma$ . ?

[SOMETHING].

Here are some references:

Singapore Lecture Notes. [SEE DANA]
Combinatorial Dichotomies of Set Theory. (BSL 2011).

Theorem [Tkachenko, 1983] Every -compact group is ccc.

Where did you get this information?

My child is interested in codes, what are some resources for them to learn more?

Introduction

Theorem 1 (Carlson-Laver, 1989). Assuming PFA, .

Theorem 2 (1985, Laver). implies , for any measure algebra .

Theorem (Hirshurn, 2000). PID implies .

Ultrapowers of Measure Algebra