 When people ask me what I do I often give the ‘sexy answer’ that I study different sizes of infinity. This usually dazzles the listener and lets me talk about why I think math is beautiful as opposed to why it is useful “for getting chicks and dollar bills”.
When people ask me what I do I often give the ‘sexy answer’ that I study different sizes of infinity. This usually dazzles the listener and lets me talk about why I think math is beautiful as opposed to why it is useful “for getting chicks and dollar bills”.
Of course when a mathematician asks me what I do I need to give a more precise answer. (Also, I feel like, to many mathematicians, the study of cardinality seems like a parlor trick. “Been there, done that.”) So I’m going to give two (easy) facts that illustrate the types of results that go past the study of cardinality and peek into the world of infinite combinatorics.
The first observation is that people in set theory and set theoretic topology are obsessed with the real numbers (affectionately, “the reals”). Often discussions start with “This fact is true of the reals, but what about in other spaces?”. (For example, the reals have a countable dense subset – the rationals – and this is important enough that we gave it a name – separable.) Often in set theoretic topology we work under the heuristic that “everything is true in the reals”, and we look for which particular topological properties give us those facts.
So, it shouldn’t be surprising that we look for copies of the reals wherever we can.
Fact 1. There is a copy of the reals inside of the partial order 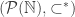
Here  means
means ![A\setminus [0, n] \subset B](https://s0.wp.com/latex.php?latex=A%5Csetminus+%5B0%2C+n%5D+%5Csubset+B+&bg=ffffff&fg=333333&s=0&c=20201002) for some
for some  . This just means that
. This just means that 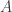 is almost contained in
is almost contained in 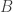 . Another way to think of this partial order is that two sets are equivalent when they differ in only finitely many places. In plainspeak, besides finitely many exceptions, every element of
. Another way to think of this partial order is that two sets are equivalent when they differ in only finitely many places. In plainspeak, besides finitely many exceptions, every element of 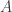 is also in
is also in 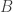 . (Also,
. (Also,  is the family of all subsets of the natural numbers.)
is the family of all subsets of the natural numbers.)
proof of Fact 1. We need to construct a family of sets  such that when
such that when 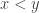 we get
we get 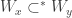 . Also, we should make sure that we didn’t construct something trivial. We should make sure that when
. Also, we should make sure that we didn’t construct something trivial. We should make sure that when 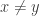 that
that 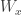 and
and 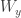 disagree on an infinite set.
disagree on an infinite set.
Fix a bijection 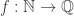 . Let
. Let  .
.
Sure enough, this has the above property that 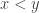 implies
implies 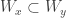 . The non triviality condition is given because whenever
. The non triviality condition is given because whenever 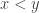 there are infinitely many rationals between
there are infinitely many rationals between  and
and  . [QED]
. [QED]
There are other things to say about this partial order (along the lines of “It contains a copy of every countable partial order”), but I will leave those for another time.
The next thing is a standard fact that is often given as a challenge exercise for undergraduates.
Fact 2. There is a family 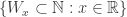 such that if
such that if 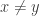 then
then 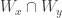 is finite.
is finite.
We will also have that each 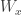 is infinite. (Can you see what happens if we don’t insist on this?)
is infinite. (Can you see what happens if we don’t insist on this?)
As a warm up, try finding an infinite (not necessarily uncountable) family with that property. (In this case you can do much better; you can make is so that the intersection of any two sets is empty.)
proof of Fact 2. Fix a bijection  . For each
. For each  , fix a sequence
, fix a sequence  of rationals that converges to
of rationals that converges to  .
.
Note that if 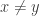 then
then  is finite, because the two sequences are converging to two different reals.
is finite, because the two sequences are converging to two different reals.
So ![\{f[S_x] : x \in \mathbb{R} \}](https://s0.wp.com/latex.php?latex=%5C%7Bf%5BS_x%5D+%3A+x+%5Cin+%5Cmathbb%7BR%7D+%5C%7D+&bg=ffffff&fg=333333&s=0&c=20201002) is the desired family. [QED]
is the desired family. [QED]
There you go! Two facts that show how infinite combinatorics goes beyond just showing that  .
.



